Dear All,
I finally can present this solution now. Yes, it is real time and common solution to all of NURBS in degree 2, 3 and 4. If you suspect about is it true? Welcome to visit my new website at Google, NURBS Intersection. Also if anyone likes to clarify the relationship in between Knots and Control-Points of NURBS then my KNOTS-EQUATION may be the best for your answer.
Enclosed is a sample piece of data for the intersection in between a cubic NURBS and a quartic NURBS for your review.
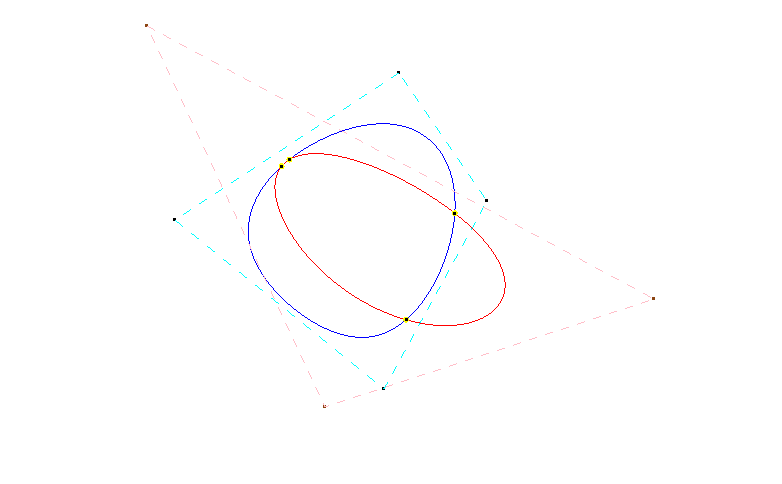
Blue NURBS -- Nonuniform, degree: 3, Ring-mode: ON;
Control points: 7;
P00(399.00, 411.00), P01(175.00, 264.00), P02(384.00, 95.00), P03(487.00, 283.00), P04(399.00, 411.00), P05(175.00, 264.00),
P06(384.00, 95.00)
Knots vector: 11;
{ 0.00, 8.00, 14.00, 21.00, 25.00, 30.00, 36.00, 43.00, 47.00, 52.00, 58.00 }
Control points of poly-Bezier: 13;
VALID (252.353275401069540, 229.526403743315510), (266.437500000000000, 190.062500000000000), (318.687500000000000, 147.812500000000000),
VALID (359.922685185185170, 146.621759259259250), (411.466666666666700, 145.133333333333330), (445.800000000000010, 207.799999999999980),
VALID (453.416161616161620, 258.143434343434310), (462.555555555555540, 318.555555555555540), (433.222222222222230, 361.222222222222230),
VALID (380.938662644544990, 360.250879839115100), (319.941176470588230, 359.117647058823540), (227.705882352941160, 298.588235294117620),
(252.353275401069540, 229.526403743315510)
Red NURBS -- Nonuniform, degree: 4, Ring-mode: ON;
Control points: 7;
P00(147.00, 458.00), P01(654.00, 185.00), P02(325.00, 77.00), P03(147.00, 458.00), P04(654.00, 185.00), P05(325.00, 77.00),
P06(147.00, 458.00)
Knots vector: 12;
{ 0.00, 9.00, 17.00, 23.00, 26.00, 34.00, 40.00, 43.00, 51.00, 57.00, 60.00, 68.00 }
Control points of poly-Bezier: 13;
VALID (502.872080911415990, 186.687972564519900), (485.208951406649650, 141.223401534526860), (378.403836317135530, 137.181457800511510), (291.944501278772350, 222.534910485933520),
VALID (276.978567774936040, 281.727398611618580), (265.754117647058820, 326.121764705882360), (294.744705882352950, 355.800588235294070), (385.528235294117680, 322.013529411764750),
VALID (448.084450127877230, 275.858491048593350), (479.362557544757010, 252.780971867007650), (503.583836317135590, 226.611457800511490), (509.495754475703390, 203.737186700767270),
(502.872080911415990, 186.687972564519900)
The intersection point(s) of above two NURBS: 4;
X00(406.013518863009610, 164.225086941131220), X01(454.788447027971420, 270.762274437878320), X02(281.568489700287840, 317.727051062005330),
X03(289.479335241518870, 324.468840895207450)
The t value(s) of X point(s) of Blue NURBS: 4;
t00 = 26.693906700333045, t01 = 30.426993447395169, t02 = 39.626960054628526,
t03 = 39.295260650722085
The t value(s) of X point(s) of Red NURBS: 4;
t00 = 29.450695691759950, t01 = 40.163956338857972, t02 = 35.487277346178828,
t03 = 35.944589350884485
Enjoy your surfing,
Hunt Chang 