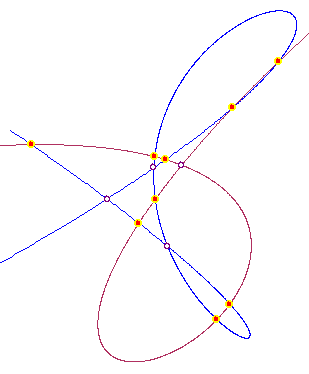
Blue Curve: degree 4, control points,
P0(365.00, 234.00), P1(702.00, 6.00), P2(15.00, 270.00), P3(800.00, 411.00), P4(321.00, 159.00); Self Intersection point at:
S0(422.623866578220830, 219.100707365751530); t[0] = 0.470568235168694, t[1] = 0.928965105280191;
S1(403.771414449105410, 206.564631127658800); t[2] = 0.033644311244951, t[3] = 0.946215379164179;
S2(428.146585044641600, 187.490098585855800); t[4] = 0.063282793880594, t[5] = 0.384577459709910;
Red Curve: degree 4, control points,
P0(289.00, 219.00), P1(619.00, 281.00), P2(433.00, 42.00), P3(244.00, 99.00), P4(566.00, 340.00);
Self Intersection point at:
S0(433.839624042999790, 220.171822083503030); t[0] = 0.169622726530818, t[1] = 0.847996997510708;
The Intersection point(s) of these two curves:
X00(373.132669769454200, 228.452384975740300), X01(422.976765319260100, 223.603384644635180), X02(427.328608685923310, 222.394565648216480);
X03(453.238364069660750, 164.255182274873330), X04(447.975296939753890, 157.993040158902660), X05(423.163860704513580, 206.415509255545150);
X06(416.528839850635050, 196.830100491660910), X07(454.443486880512640, 243.396391744401060), X08(472.693821439787600, 261.766619105502170);
Blue Curve's t value(s):
t[00] = 0.006206970900832, t[01] = 0.482580691766434, t[02] = 0.924118404044710;
t[03] = 0.115684858451726, t[04] = 0.278944240069076, t[05] = 0.436819858435325;
t[06] = 0.047883985834167, t[07] = 0.888939387836823, t[08] = 0.847857157064769;
Red Curve's t value(s):
t[00] = 0.076900012265960, t[01] = 0.147590072801383, t[02] = 0.155924661830965;
t[03] = 0.398565884526332, t[04] = 0.426824837981717, t[05] = 0.824218211537170;
t[06] = 0.806057750545920, t[07] = 0.883703196233528, t[08] = 0.909078781554686;
|  |