Archives Discussions
- AMD Community
- Communities
- Developers
- Devgurus Archives
- Archives Discussions
- A fast and precise INTERSECTION solution of cubic ...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
A fast and precise INTERSECTION solution of cubic BEZIER curves
Cubic Bezier curve has been invented over fifty years, but its usage was serious limited as there is no effective way to solve its intersection points problem either in between curve-to-curve or within a curve itself.
I have worked out a fast, precise and by theory solution to find out all of the INTERSECTION points. I wonder if AMD is interested to license this solution to enlarge her code library.
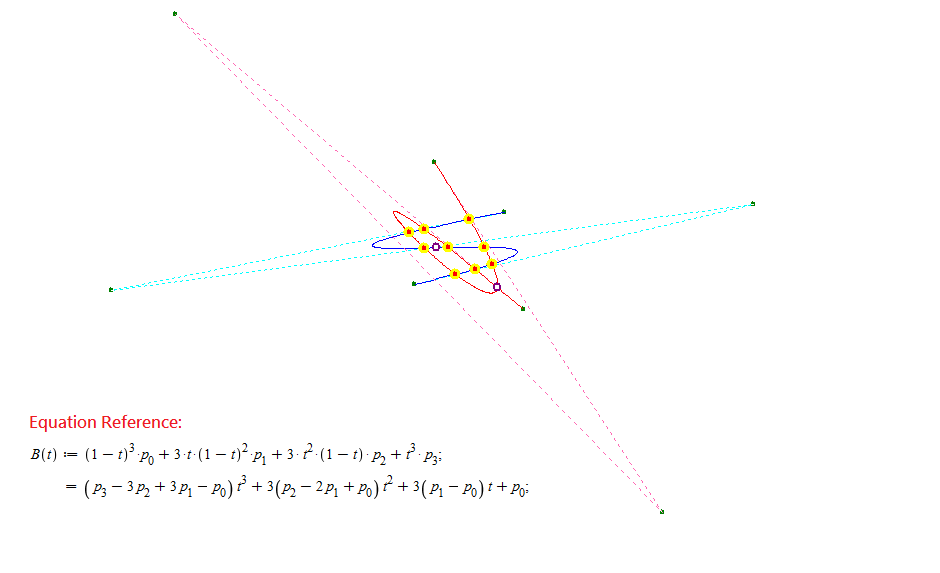
Enclosed are a picture of cubic Bezier curves’ intersection points and certain data related with the two curves for any person who feels interested to verify their corectness.
Hunt Chang
Ps. my solution is direct and by theory, not an approach of approximation like bisection or bez-clipping or others.
Blue Curve control points: P0 (504.000000, 360.000000), P1 (111.000000, 282.000000), P2 (753.000000, 368.000000), P3 (414.000000, 288.000000);
Inflection point(s) at (436.247939291, 324.686418634); t[0] = 0.493948130;
Red Curve control points: P0 (434.000000, 410.000000), P1 (662.000000, 60.000000), P2 (175.000000, 558.000000), P3 (523.000000, 263.000000);
Self Intersection point at (497.178713708, 284.716993708); t[1] = 0.219641391, t[2] = 0.973625079;
The Intersection point(s) of those two curves:
(469.284632332, 352.984190733), (484.205333013, 325.417398792), (491.920199738, 308.486201692), (455.137674488, 298.118444831);
(424.123514673, 324.385358688), (408.647917012, 339.640827151), (447.698139089, 324.971794242), (423.836163179, 343.202129023);
(474.615957980, 303.350537381);
Blue Curve's t value(s):
t[0] = 0.032102241, t[1] = 0.614547187, t[2] = 0.892283373, t[3] = 0.953489452;
t[4] = 0.464196010, t[5] = 0.110969242, t[6] = 0.521571699, t[7] = 0.086657188;
t[8] = 0.924926429;
Red Curve's t value(s):
t[0] = 0.063739442, t[1] = 0.105845537, t[2] = 0.139708529, t[3] = 0.428695394;
t[4] = 0.532211221, t[5] = 0.592534208, t[6] = 0.909201381, t[7] = 0.864858712;
t[8] = 0.947179525;
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Guess I might be jumping too fast to cubic intersection points directly. Here is another quadratic Bezier curves' intersection example. Anyone feel interested may use Excel spreadsheet for verification, it is quick and easy to do than the other tool.![]()
Hunt Chang
Blue Curve control points: P0 (459.000000, 478.000000), P1 (238.000000, 211.000000), P2 (449.000000, 356.000000);
Red Curve control points: P0 (435.000000, 226.000000), P1 (271.000000, 522.000000), P2 (466.000000, 444.000000);
The Intersection point(s) of those two curves:
(438.959511410, 453.539658178), (370.941994513, 363.539928912), (388.652300986, 318.014288962);
Blue Curve's t value(s):
t[0] = 0.047550353, t[1] = 0.271012112, t[2] = 0.826003935;
Red Curve's t value(s):
t[0] = 0.925565288, t[1] = 0.282887514, t[2] = 0.174713879;
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
To: R&D experts of AMD,
Not to boast myself, but if I do not speak for my own solution then nobody can.
People asked me about what is the better of my solution than the other solutions that already exists?
First off, I guess my solution so far is the only one in the whole-world which solved the intersection points problem of cubic and quadratic Bezier curves accurately by Geometry theory instead of by way of approximation. Frankly the way of approximation has nothing wrong as soon as it can get the correct answer; but compare to the same level of data accuracy or precision, I believe mine is much faster. Although my way to solve the problem is also a complicate process, but it is still fast enough to be operated in real-time even by an AMD Athlon(K5) CPU. May be someone would defy me for bluffing, please take a few minutes of calculation to verify the data I already presented here, just let those data speaking for the truth.
Secondly, cause in each intersection point there must be two ‘t’ values (or more by coincidence) get involved, so we can get (at least) two sets answers of coordinates from each intersection. In theory, when an intersection exists, the two sets of coordinate must be exactly the same, but in reality of computation there are certain deviation exists most of the time. Under a reasonable coordinate setting, my data deviation is always lower than the constant of FLT_EPSILON; actually I had done some random control points location tests, over 97% of my data deviation are lower than 1.0e-10 and only less than 0.3% deviation are within the range of FLT_EPSILON ~ 1.0e-08. Since my solution is by Geometry theory, it means if I change the code to use 16-byte-doulbe-precision format number in the future then the data precision would be double as well; and its extra CPU overhead would be quite small.
Lastly, during the very long period I spent to discover this solution, I did find some math properties of the curve that never have been exposed before; actually I count on them to solve the 2D curve intersection puzzle. So, even I do not know what kind of algorithm or strategy you are using to solve the B-spline-surface intersection problem now, but I think my solution or my discovery may offer you a better chance or a different approach to look at that problem.
If you are interested on my solution, feel free to contact me.
Hunt Chang
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Quartic X Cubic Bezier Curves
People asked me is this really possible?!
Please check the data and let them talk.
Hunt Chang
Blue Curve control points:
P0(294.000000, 478.000000), P1(710.000000, 313.000000), P2(461.000000, 159.000000), P3(352.000000, 482.000000);
Red Curve control points:
P0(321.000000, 445.000000), P1(666.000000, 384.000000), P2(220.000000, 378.000000), P3(663.000000, 80.000000), P4(442.000000, 486.000000);
The Intersection point(s) of those two curves:
(370.002329784, 435.470577799), (403.556382661, 427.160436924), (460.864511925, 391.115205214), (464.260893656, 308.774187728);
(501.914020196, 293.066503440), (496.828922444, 360.676524395);
Blue Curve's t value(s):
t[0] = 0.948066352, t[1] = 0.104508914, t[2] = 0.183598275, t[3] = 0.705242235;
t[4] = 0.587258396, t[5] = 0.257514275;
Red Curve's t value(s):
t[0] = 0.040947602, t[1] = 0.078958480, t[2] = 0.238408796, t[3] = 0.525974506;
t[4] = 0.777083037, t[5] = 0.898521787;